The chain collocation method: A spectrally accurate calculus of forms¶
The figures below were used in the paper published here.
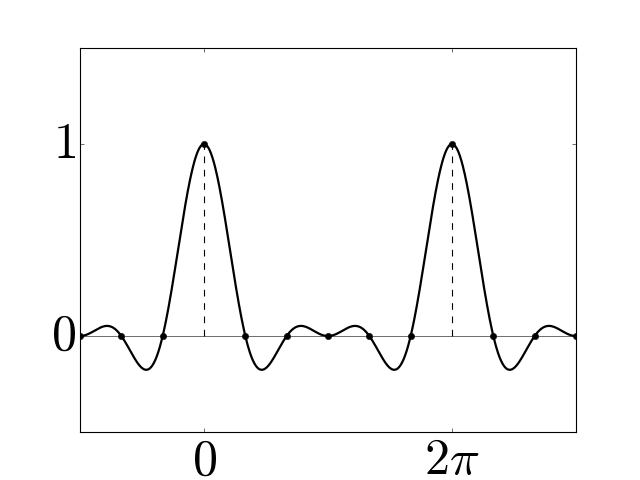
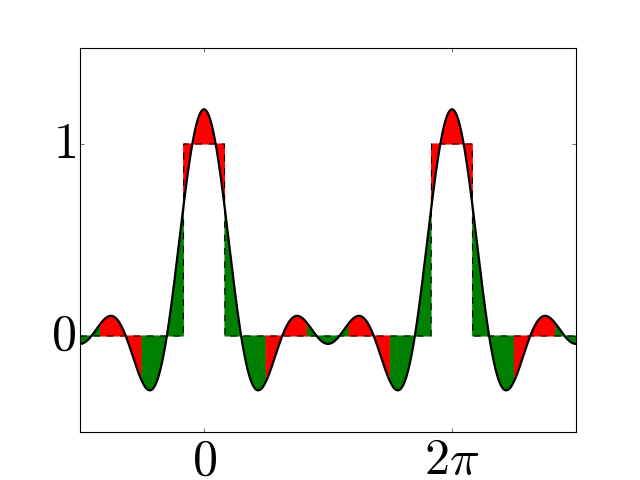
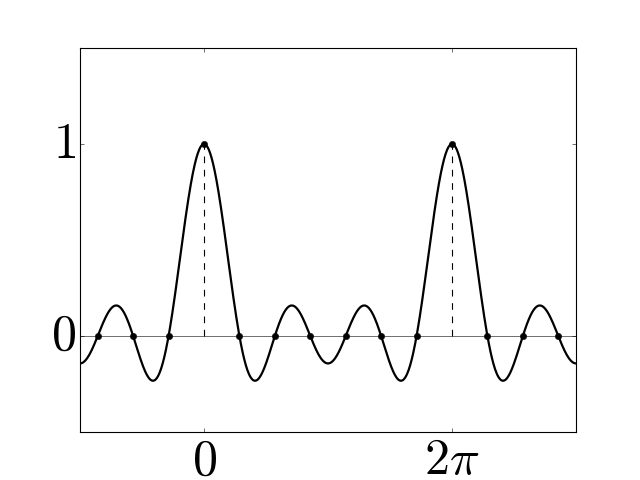
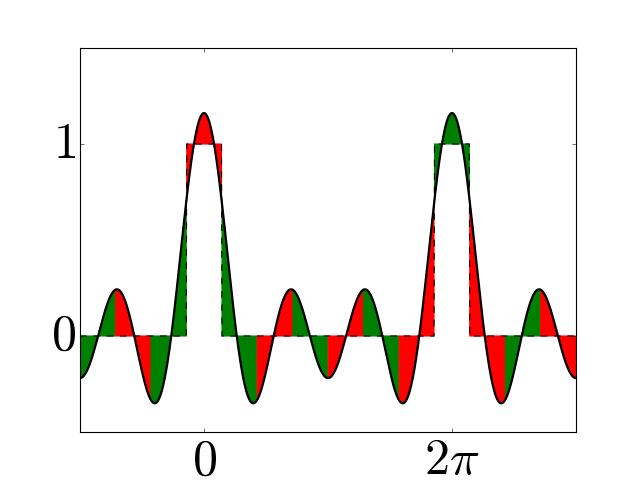
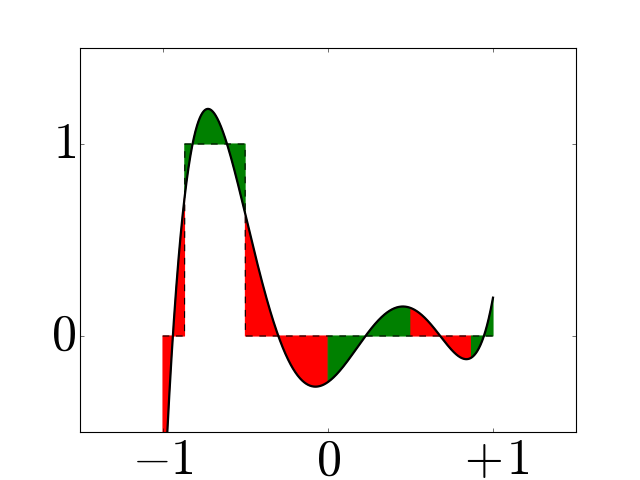
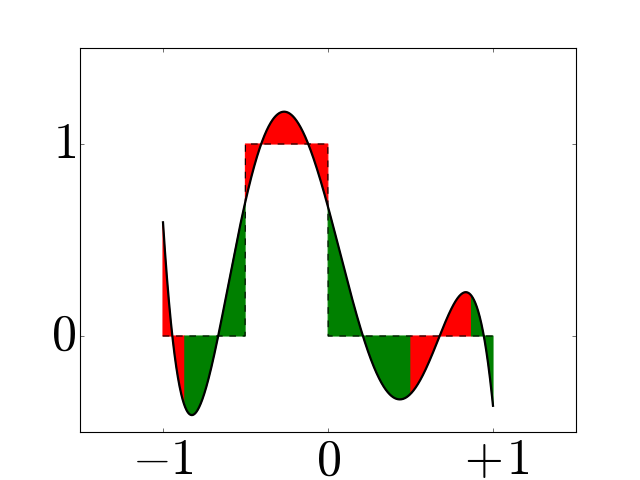
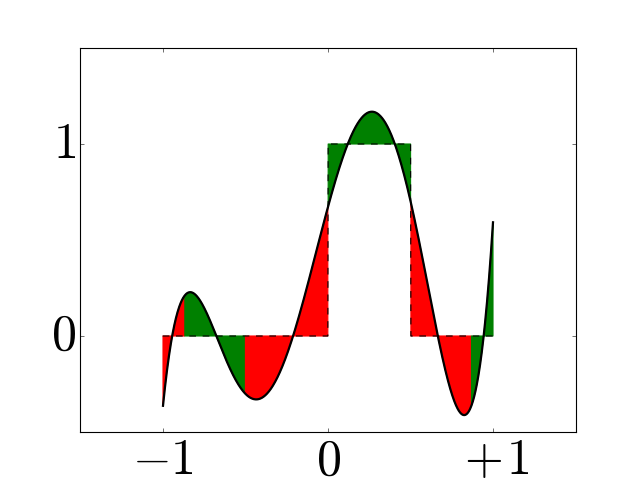
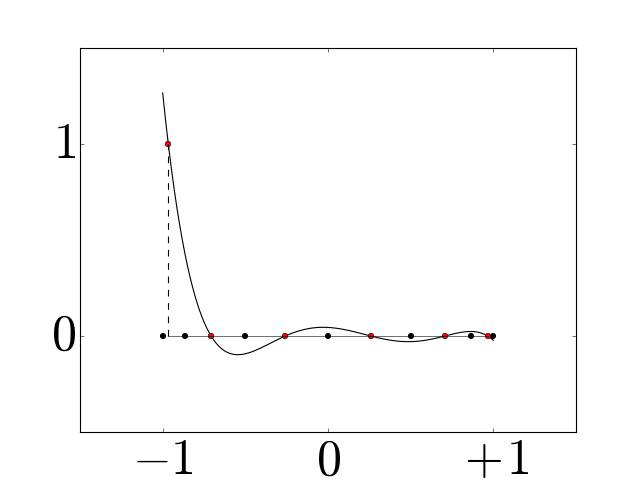
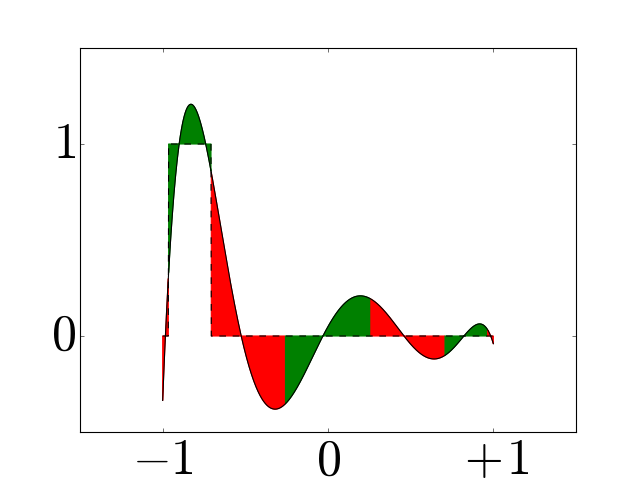
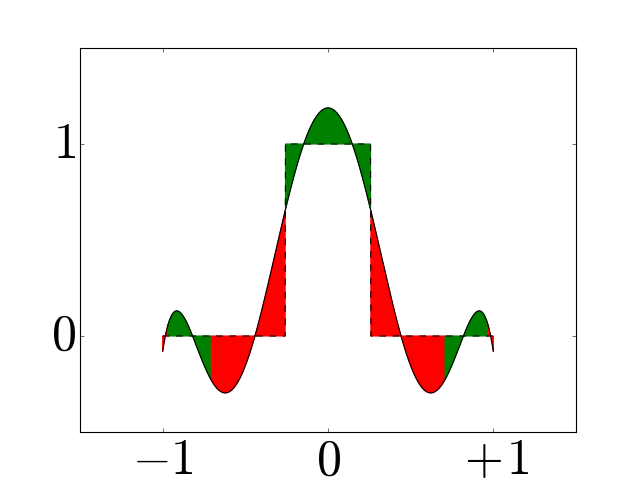
Figure 3¶
Examples of periodic interpolators for \(N=6\) (a) and \(7\) (b), and corresponding periodic histopolators (c) and (d), scaled by \(h=2\pi/N\) for clarity. While the interpolator \(\alpha_N\) satisfies \(\alpha_N(nh \mod 2\pi) = \delta_{0n} \; \forall n\), the histopolator \(\beta_N\) integrates to \(1\) over the dual cell straddling \(x=0\), and to \(0\) over other dual cells in the range \([0,2\pi]\). Note that the alternating red and green colors are used to mark out dual cells, and to illustrate that the integral of \(\beta_N\) over each of these dual cells sums to zero or one.
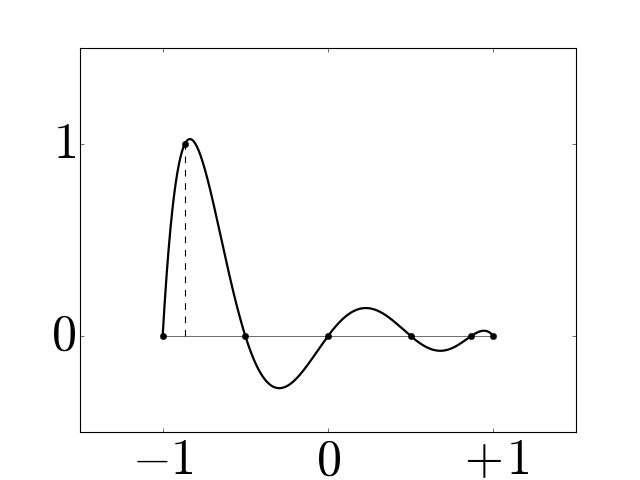
Figure 5¶
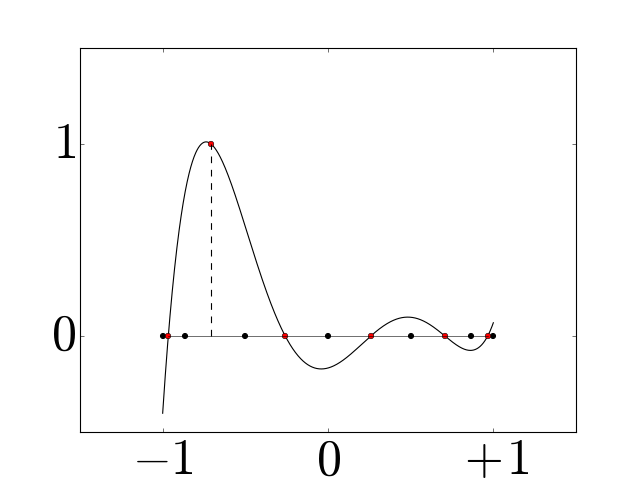
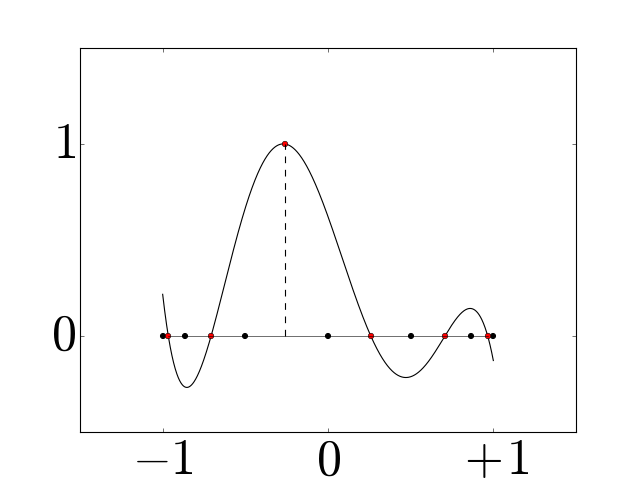
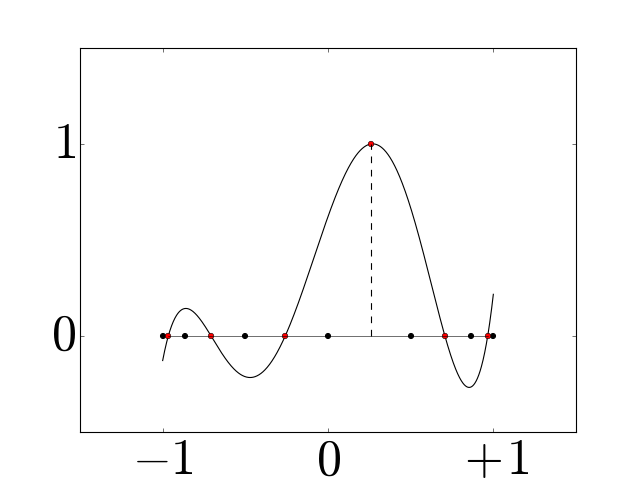
Chebyshev primal basis functions for a grid with \(N=7\). We normalize the one-form basis functions by \(x_n\!-\!x_{n-1}\) to have approximately the same scale in our visualizations.
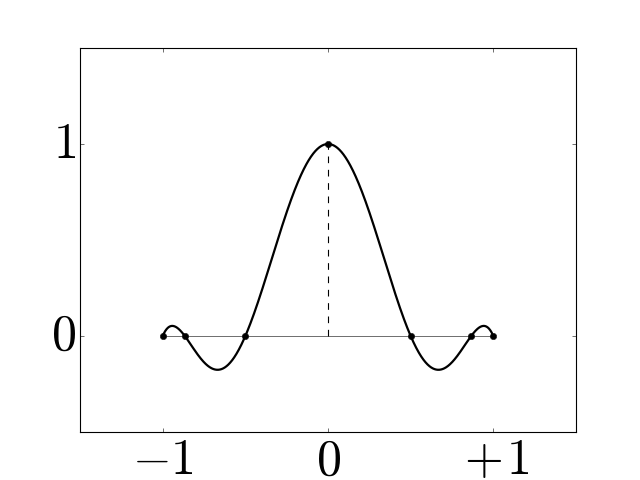
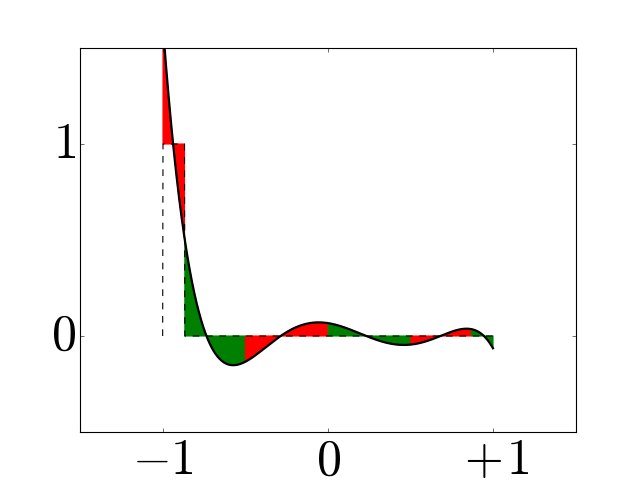
Figure 6¶
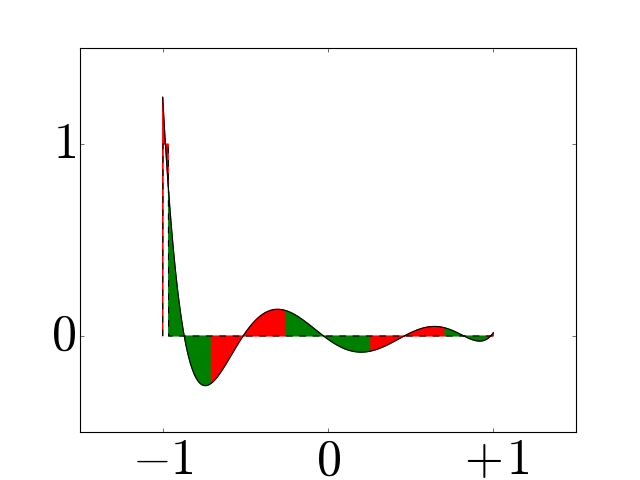
Chebyshev dual basis functions for a grid with \(N=7\).
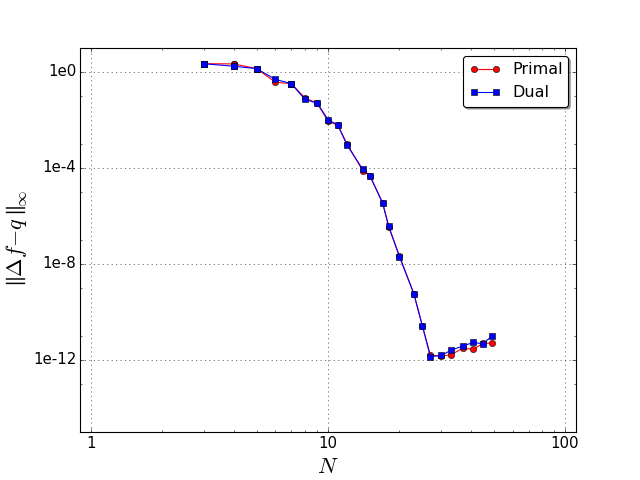
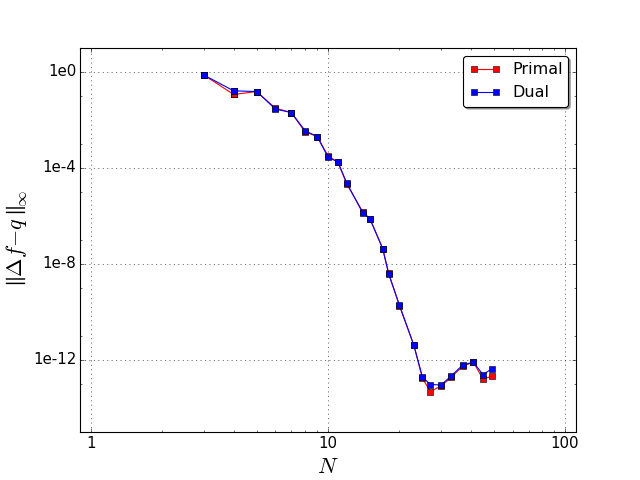
Figure 7¶
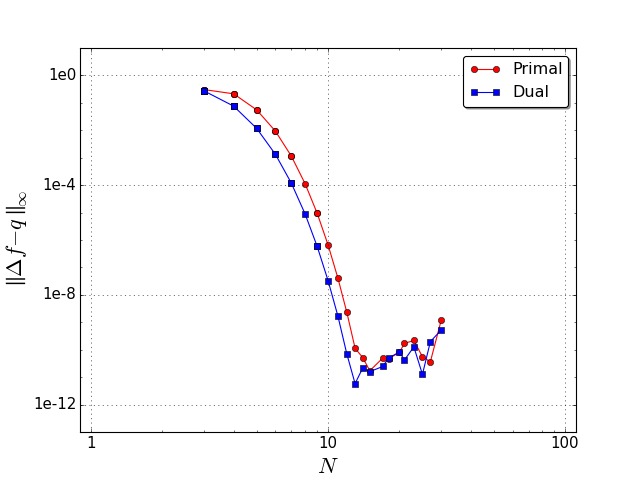
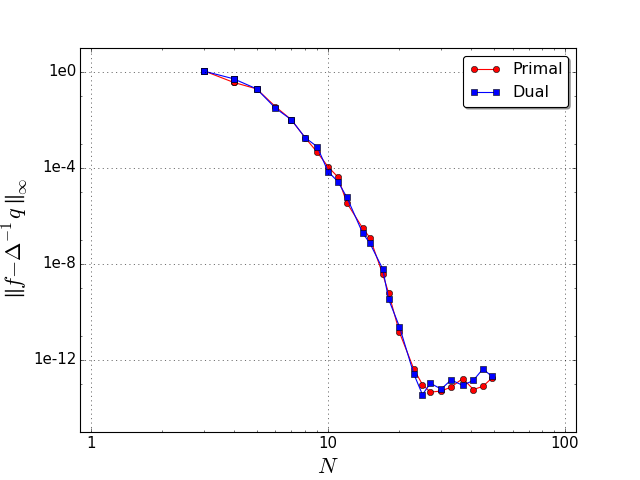
Convergence graphs for a 1D Poisson equation: (a) we solve \(\Delta f = e^{\sin x} (\cos^2 x - \sin x)\) on a periodic domain for either a primal, or dual \(0\)-form \(f\); (b) we solve math:Delta f = e^{x} on a Chebyshev grid, for either a primal \(0\)-form with Dirichlet boundary conditions \(f(-1)=e^{-1}\) and \(f(1)=e\), or for a dual \(0\)-form with Neumann boundary conditions math:f^prime(-1)= e^{-1} and \(f^\prime(+1)= e\). All of our results exhibit spectral convergence (measured through the \(L^\infty\) error \(\|f - \Delta^{-1}q \|_\infty\)), with the conventional plateau when we reach the limit of accuracy of the representation of floating point numbers.
(Source code, png, hires.png, pdf)
(Source code, png, hires.png, pdf)
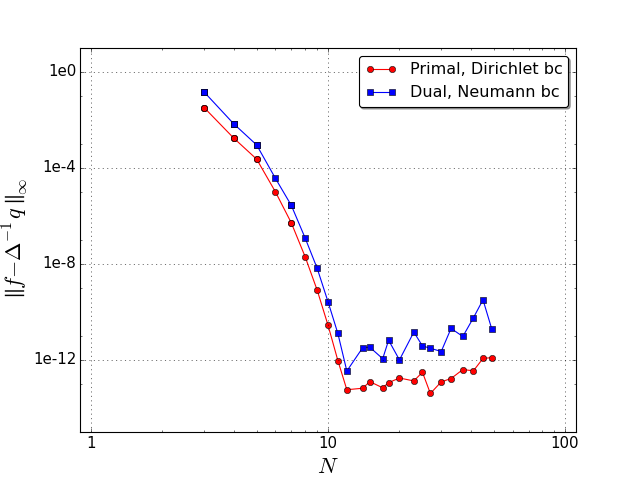
Figure 8¶
Convergence graphs for a 2D Poisson equation; (a) we solve \(\Delta f = e^{\sin x} (\cos^2 x - \sin x)+e^{\sin y} (\cos^2 y - \sin y)\) on a periodic domain for either a primal, or dual \(0\)-form \(f\); (b) Now for \(\Delta f = e^{\sin x} (\cos^2 x - \sin x) \mathbf{d}x +e^{\sin y} (\cos^2 y - \sin y) \mathbf{d}y\); (c) we solve \(\Delta f = e^{x}+e^{y}\) on a Chebyshev grid, for either a primal \(0\)-form with Dirichlet boundary conditions \(f(x,y)=e^{x}+e^{y}\), or for a dual \(0\)-form with Neumann boundary conditions \(\nabla f(x) \cdot \mathbf{n} = (e^x\;e^y)^t \;\mathbf{n}\); (d) Now for \(\Delta f = e^{x} \mathbf{d}x+e^{y}\mathbf{d}y\). All of our results exhibit spectral convergence (measured through the \(L^\infty\) error \(\|\Delta f - q \|_\infty\)), with the conventional plateau in accuracy for fine meshes.
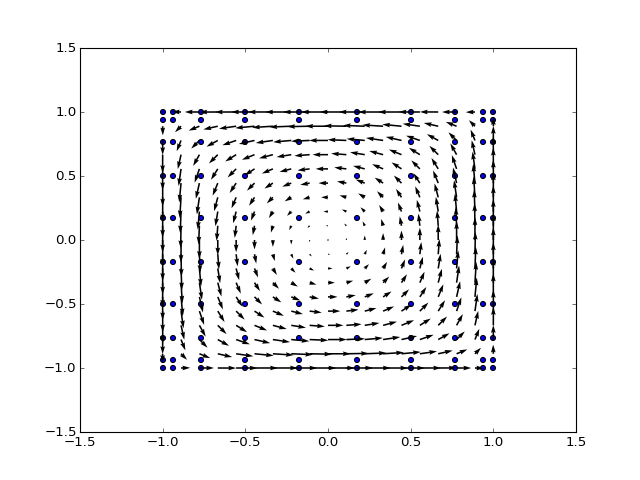
Figure 9¶
Plot for the solution of \((\star\mathbf{d}\star\mathbf{d}+\mathbf{d}\star\mathbf{d}\star)f\!=\!0\) with the boundary conditions of \(\star f |_{\mathcal{B}} = 0\) (vector field is tangent to the boundary) and \(\star\mathbf{d}\star f |_{\mathcal{B}}\!=\!1\) (the curl at the boundary is equal to \(1\)). The domain is \([-1,1]^2\), discretized by a \(10\!\times\!10\) Chebyshev grid.
(Source code, png, hires.png, pdf)